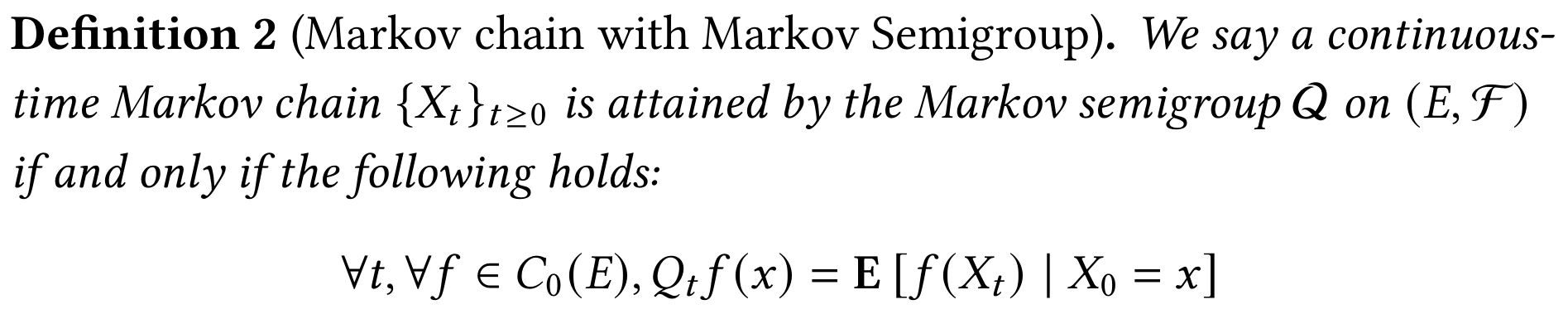Skip to content

Markov Semigroup

约 978 个字 2 张图片 预计阅读时间 5 分钟

定义

上一节中 对 diffusion 的描述侧重于每一步的随机变量 \(X_t\)。也可以像 Markov chain 中的转移矩阵一样刻画。

将 Markov chain 中的转移矩阵 \(P\) 看作是作用在概率分布函数 \(\pi_t\) 上的线性算子，进而推广到连续的 diffusion 上。（线性算子 \(\rightarrow\) 半群）

定义：

  1. 对样本空间中的每一个 \(x\)，\(Q_t(x)\) 为测度空间 \((E, \mathcal{F})\) 的一个测度（可以理解为一个从 \(x\) 转移到其他状态上的概率分布）
  2. \(\delta _x\) 为狄拉克测度，表示在 \(t = 0\) 时，系统还没有演化，状态还是 \(x\) 本身。
  3. 记忆无关性：从 \(x\) 出发经过 \(s + t\) 的时间，等价于先从 \(x\) 出发经过 \(s\) 的时间到达某个 \(y\)，再经过 \(t\) 的时间到达最终状态。
  4. \(Q_t(x, \cdot)\) 表示从状态 \(x\) 经过时间 \(t\) 后到达某个集合的概率
  5. \(Q_t(x, \mathrm{d}y)\)：描述转移到一个无穷小区域的概率，可以被积分，如对集合 \(A\)，有 \(Q_t(x, A) = \int_{A}Q_t(x, \mathrm{d}y)\)（这里是对 \(A\) 上所有 \(\mathrm{d}y\) 进行积分）
  6. \(Q_t\) 就相当于 Markov chain 中的转移矩阵 \(P\) 的 \(t\) 次方，不过 \(t\) 由离散变为连续的了。

另一种定义描述

设 \( (P_t)_{t \geq 0} \) 是一族作用在某个函数空间（通常是某个测度空间上的可测函数空间，例如 \( L^p \) 空间）上的线性算子。这个算子族称为一个马尔可夫半群，如果满足以下条件：> J

  1. 初始条件：\( P_0 \) 是恒等算子，即 \( P_0 f = f \) 对于所有的 \( f \) 都成立。> J
  2. 半群性质：对任意的 \( s, t \geq 0 \)，有 \( P_{s+t} = P_s \circ P_t \)（即算子 \( P_s \) 和 \( P_t \) 的复合等于 \( P_{s+t} \)）。> J
  3. 马尔可夫性：对所有非负函数 \( f \) 和任意 \( t \geq 0 \)，有 \( P_t f \geq 0 \)，并且如果 \( f \) 是一个概率密度函数（即 \( \int f(x) \, dx = 1 \)），那么 \( P_t f \) 也是一个概率密度函数。

\(Q_t\) 也可以被理解为一个函数到函数的映射：

\[ Q_t(f)(x) = \int_{y \in E}^{} f(y)Q_t(x, \mathrm{d}y) \]

Markov Chain With Markov Semigroup

定义：

  • \(C_0(E)\)：在无穷处趋于 0 的连续函数构成的集合

如果还满足：

  • \(\forall t \ge 0, \forall f \in C_0(E), Q_t(f) \in C_0(E)\)
  • \(\forall f \in C_0(E), ||Q_tf - f||_{\infty} \rightarrow 0 \space \text{as}\space t \rightarrow 0\)

那么称半群 \(\mathcal{Q}\) 为 Feller semigroup。

Chapman-Kolmogorov equation

\(Q\) 是一个 \((E, \mathcal{F})\) 上的马尔可夫半群，那么对任何 \(f \in C_0(E)\)，有 \(Q_{s+t}(f) = Q_sQ_t(f)\)。

利用 \(Q_t\) 的性质易证。

Generator of the Markov Semigroup

设 \(Q\) 是一个 \((E, \mathcal{F})\) 上的 Markov semigroup，定义 \(\mathcal{L}\) 为 \(Q\) 的 generator 当且仅当

\[ \mathcal{L}f = \lim_{t \downarrow 0} \frac{Q_tf - f}{t} \]

对任意 \(f \in D(\mathcal{L}) := { f \in C_0(E) : \text{the aboce limit exists} }\) 成立。

可以得到

  • \(\mathcal{L} = \frac{\mathrm{d}}{\mathrm{d}t}Q_t|_{t=0}\)，因此 \(\mathcal{L}\) 是算子族 \(\{ Q_t\}_{t\ge 0}\) 的“变化率”
  • \(Q_t = e^{t \mathcal{L}}\) 对任意 \(t\) 成立。（正如离散马尔可夫链中 \(P^t\) 仅由最初的 \(P\) 导出一样）
  • \(\mathcal{L}\) 和 \(Q_t\) 是可交换的：\(Q_t \mathcal{L} = \mathcal{L} Q_t\)

直观理解：马尔可夫半群的生成元描述极短时间内分布状态的变化，因而可以通过积分等方式刻画长时间的变化，或者刻画瞬时状态。

举例：

  • 泊松过程的 generator：可以得出 \(\mathcal{L}f(n) = \lambda (f(n+1) - f(n))\)，因此 Poison process 的 generator 为一个主对角线上全为 \(-\lambda\)，超对角线上全为 \(\lambda\) 的无穷大矩阵
  • Itô process (diffusion) 的 generator：\(\forall f \in C_0(E), \mathcal{L}f = f'\mu + \frac{1}{2}f''\sigma ^2\)
  • 立即可以得出，standard Brownian motion 的 generator 为 \(\mathcal{L}f = \frac{1}{2}f''\)