Skip to content

Brownian Motion

约 1057 个字 1 张图片 预计阅读时间 5 分钟

定义

Standard Brownian Motion (1)

对随机过程 \(\{ W(t)\}_{t \ge 0}\)，如果满足

  • \(W(0)=0\)
  • Independent Increments: \(\forall 0 \le t_0 \le \cdots \le t_n\)，\(W(t_1) - W(t_0), \ldots, W(t_n) - W(t_{n-1})\) 互相独立
  • Stationary Increments: \(\forall s, t > 0, W(s+t) - W(s) \sim \mathcal{N}(0, t)\)
  • \(W(t)\) is continuous almost surely.（记 \(\Omega\) 为样本空间，那么 \(W\) 可以看作是从 \(\mathbb{R} \times \Omega\) 到 \(\mathbb{R}\) 的一个映射；continuous almost surely 表示 \(\exists \Omega_0 \in \Omega\) with \(\mathrm{Pr}[\Omega_0] = 1\) 使得 \(\forall \omega \in \Omega, W(t, \omega)\) 关于 \(t\) 是连续的）

则称该随机过程为 Standard Brownian Motion / Wiener process。

显然，\(W(t) \sim \mathcal{N}(0, t)\)。

Gaussian Process

一个随机过程 \(\{ X_t\}_{t \ge 0}\) 如果满足对任意 \(0 \le t_1 \le \cdots \le t_n\)，都有向量 \((X(t_1), X(t_2), \ldots, X(t_n))\) 服从 Gaussian 分布，则称之为 Gaussian Process。

可以用以下方法来判断高维向量是否服从高斯分布：一个向量 \((X(t_1), X(t_2), \ldots, X(t_n))\) 服从高斯分布当且仅当 \(\forall (a_1, a_2, \ldots, a_n), \sum_{i=1}^{n}a_iX_i\) 服从高斯分布。

Standard Brownian Motion (2)

一个随机过程 \(\{ W(t) \}_{t \ge 0}\)，如果满足

  • \(\{ W(t) \}_{t \ge 0}\) 是一个几乎连续的 Gaussian process
  • \(\forall s \ge 0, E[W(s)] = 0\)
  • \(\forall 0 \le s\le t, \operatorname{Cov}(W(s), W(t)) = s\)

则称之为 standard Brownian motion / Wiener process。

第三个条件说明，两个不同的时间处的随机变量的相关关系正比于较小的时间，且较小的时间越大，相关性越大。直观上理解：在时间 \(s\) 之后的过程，可以看作是以时间 \(s\) 为“零点”出发的新布朗运动，所以相关性只应该和初始状态有关。对于同一个 \(t\)，如果 \(s\) 越大，则 \(t - s\) 越小，间隔的时间越短，自然相关性就越高。

可以证明，standard Brownian motion 的两个定义是等价的，后者更容易用于判别。

Other Notations

  • \(\Phi(\cdot)\)：\(\mathcal{N}(0,1)\) 的 CDF
  • \(f_t(\cdot)\)：\(\mathcal{N}(0, t)\) 的概率密度
  • 对任意 \(t_1 \le t_2 \le \ldots \le t_n\)，\(W(t_1), \ldots, W(t_n)\) 的联合概率分布 \(f(x_1, \ldots, x_n) = f_{t_1}(x_1)f_{t_2 - t_1}(x_2 - x_1) \cdots f_{t_n - t_{n-1}}(x_n - x_{n-1})\)
  • 对 \(0 \le s \le t\)，\(f_{s|t}(x|y)\)：条件 \(X(t) = y\) 下 \(X(s) = x\) 的概率，服从 \(\mathcal{N}(ys/t, s(t-s)/t)\) 的 Gaussian 分布
\[ f_{s|t}(x|y) = \frac{f_s(x)f_{t - s}(y - x)}{f_t(y)} = C \cdot \exp \left( -\frac{(x - ys/t)^2}{2s(t-s)/t} \right) \]
  • 对 Standard Brownian Motion \(\{ W(t) \}_{t \ge 0}\)，如果 \(\{ X_t \}_{t \ge 0}\) 满足 \(X(t) = \mu t+\sigma W(t)\)，那么称 \(\{ X_t\}_{t \ge 0}\) 为一个 \((\mu, \sigma^2)\) Brownian motion。显然，\(X(t) \sim \mathcal{N}(\mu t, \sigma^2 t)\)。

Hitting Time

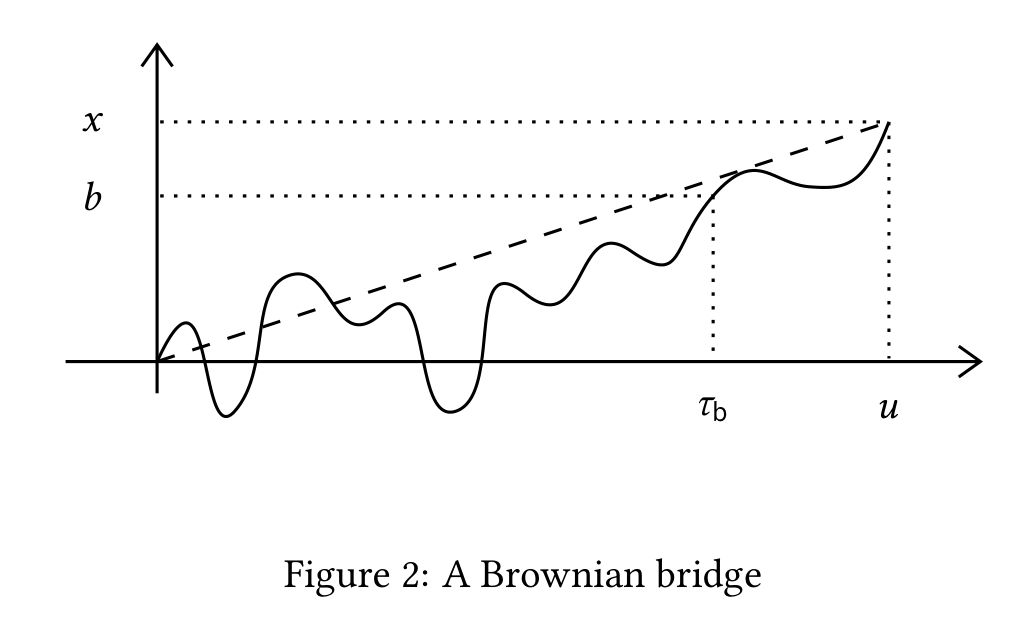
对位置 \(b\)，定义 \(\tau _b = \inf \{ t \ge 0 \mid W(t) > b \}\)，有

\[ \begin{align*} \mathrm{Pr}[\tau _b < t] &=\mathrm{Pr}[\tau _b < t \land W(t) > b] + \mathrm{Pr}[\tau _b < t \land W(t) < b] \\ &= \mathrm{Pr}[W(t) > b] + \mathrm{Pr}[W(t) < b \mid \tau _b < t]\mathrm{Pr}[\tau _b < t] \end{align*} \]

而

\[ \mathrm{Pr}[W(t) > b] = \mathrm{Pr}\left[\frac{W(t)}{\sqrt{t}} > \frac{b}{\sqrt{t}}\right] = 1 - \Phi\left(\frac{b}{\sqrt{t}}\right) \]

且当已知 \(\tau _b < t\) 时，原布朗运动中从 \(t\) 开始以后的过程可以再次看作一个新的布朗运动，故有

\[ \mathrm{Pr}[W(t) < b \mid \tau _b < t] = \frac{1}{2} \]

可计算出

\[ \mathrm{Pr}[\tau _b < t] = 2\left(1 - \Phi\left(\frac{b}{\sqrt{t}}\right)\right) \]

Brownian Bridge

在 Other Notations 一节中，计算了当 \(W(u)=x\) 已知时的 \(W(t)\space(t \le u)\)，把这段随机过程重新记为 \(X(t)\)，并称之为 Brownian Bridge:

已经得出了 \(X(t) \sim \mathcal{N}(tx/u, t(u-t)/u)\)，也就是说，\(X(t)\) 的均值在 \((u,x)\) 和原点的连线上，方差随距两段的距离减小而减小。

对任何 \(0 \le s \le t \le u\) 可以计算得到：

\[ \begin{align*} \operatorname{Cov}(X(t), X(s)) &= \operatorname{Cov}(W(t), W(s) \mid W(u) = x) \\ &= \mathbf{E}[W(t) \cdot W(s) \mid W(u) = x] - \mathbf{E}[W(t) \mid W(u) = x] \mathbf{E}[W(s) \mid W(u) = x] \\ &= \int_{-\infty}^{\infty}y \mathbf{E}[W(s) \mid W(t) = y, W(u) = x]\cdot f_{W(t)|W(u)}(y|x)\mathrm{dy} - \frac{st}{u^2}x^2 \\ &= \frac{s}{t} \mathbf{E}[W(t)^2\mid W(u)=x] - \frac{st}{u^2}x^2 \\ &= \frac{s(u-t)}{u} \end{align*} \]

Standard Brownian Bridge

一个以 \(W(1)=0\) 结束的 standard Brownian motion 称为 standard Brownian bridge。

此时有

  • \(X(t) \sim \mathcal{N}(0, t(1-t))\)
  • \(\operatorname{Cov}(X(t), X(s)) = s(1-t), \space 0 \le s \le t \le 1\)