Energy-Based Model (EBM)
约 717 个字 7 张图片 预计阅读时间 4 分钟
设 \(P_{\theta}(x)=\frac{1}{Z(\theta)}g_{\theta}(x)\),其中 \(Z(\theta)=\int g_{\theta}(x) \, dx\),\(g_{\theta}\) 有非常灵活的选择,一般选择较为简单的,可以计算积分的,然后用这种较小的块去搭建更大、更复杂的模型,例如
- Autoregressive:products of normalized objects \(P_{\theta}(x)P_{\theta'(x)}(y)\)
\[ \int _{x} \int _{y}P_{\theta}(x)P_{\theta'(x)}(y) \, dy \, dx= \int _{x}P_{\theta}(x) \, dx = 1 \]
- Latent variables:Mixture of normalized objects \(\alpha P_{\theta}(x) + (1-\alpha) P_{\theta'}(x)\)
\[ \int _{x}\alpha P_{\theta}(x) + (1-\alpha)P_{\theta'}(x) \, dx =\alpha + (1-\alpha) = 1 \]
一般选择令
\[ P_{\theta}(x) = \frac{1}{Z(\theta)}\exp f_{\theta}(x) \]
\(Z(\theta)=\int _{x}\exp f_{\theta}(x) \, dx\) 称为 partition function,当维度太高时,基本无法计算
Training
目标:最大化 \(\frac{\exp \{ f_{\theta}(x_{train}) \}}{Z(\theta)}\),即让分母尽可能小,分子尽可能大
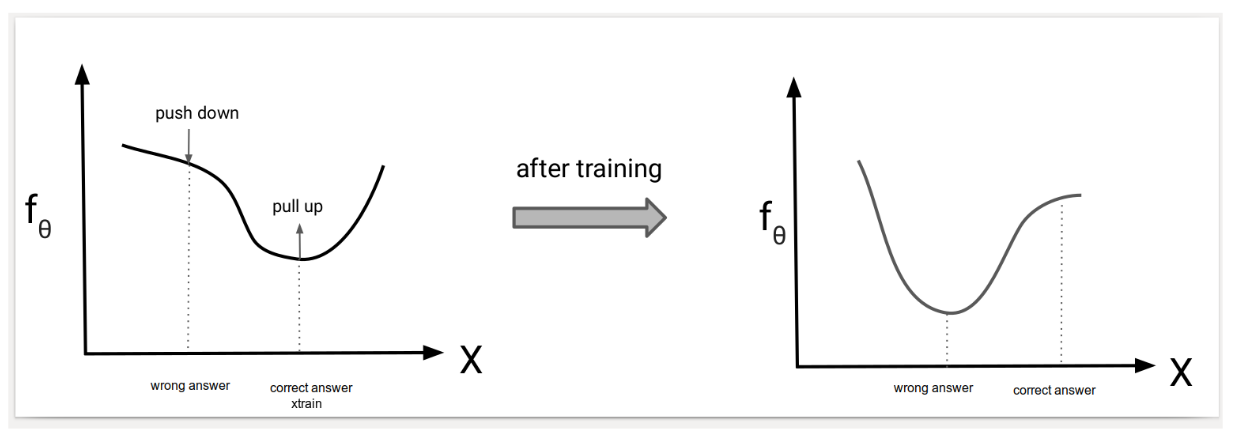
Contrastive Divergence
由于 \(Z(\theta)\) 很难算出,可以用 MC 估计:采样 \(x_{sample}\) 服从 \(P_{\theta}\) ,计算
\[ \nabla_{\theta}(f_{\theta}(x_{train})- f_{\theta}(x_{sample})) \]
称为 Contrastive divergence,推导:
\[ \begin{align} & \quad \nabla_{\theta}\log \frac{\exp \{ f_{\theta}(x_{train}) \}}{Z(\theta)} \\ & =\nabla_{\theta}f_{\theta}(x_{train}) - \nabla_{\theta}\log Z(\theta) \\ & =\nabla_{\theta}f_{\theta}(x_{train}) - \frac{\nabla_{\theta}Z(\theta)}{Z(\theta)} \\ & =\nabla_{\theta}f_{\theta}(x_{train}) - \frac{1}{Z(\theta)}\int_{x} \nabla_{\theta}\exp \{ f_{\theta}(x) \} \,dx \\ & =\nabla_{\theta}f_{\theta}(x_{train})-\frac{1}{Z(\theta)}\int _{x}\exp \{ f_{\theta}(x) \} \nabla_{\theta}f_{\theta}(x) \, dx \\ & =\nabla_{\theta}f_{\theta}(x_{train})-\int_{x} \frac{\exp \{ f_{\theta}(x) \}}{Z(\theta)} \nabla_{\theta}f_{\theta}(x) \\ & = \nabla_{\theta}f_{\theta}(x_{train})-\mathbf{E}_{x \sim x_{sample}}[\nabla_{\theta}f_{\theta}(x)] \\ & \approx \nabla_{\theta}f_{\theta}(x_{train}) - \nabla_{\theta} f_{\theta}(x_{sample}) \end{align} \]
这里 \(x_{sample} \sim P_{\theta}(x) = \frac{\exp(f_{\theta}(x))}{Z(\theta)}\),难以取样得到,可以采用下述两个迭代算法:


都需要迭代取样,非常慢。可以改进为 training without sampling,使用 score function:
\[ s_{\theta}(x)=\nabla_{x}\log p_{\theta}(x)=\nabla_{x} f_{\theta}(x) \]
也就是计算对数化之后的梯度,可视化:
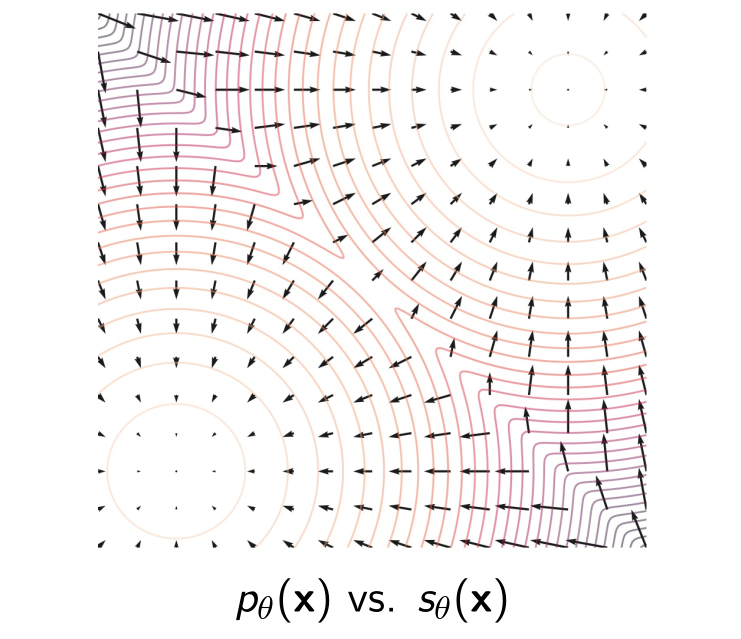
Score Matching
参考 Score-Matching
直观上看,就是想要先让梯度近似相等,然后在除以 partition function \(Z(\theta)\) 的时候并不会影响梯度,那么两个分布就应该很接近了。最终结果:
\[ \begin{align} D_{F}(p_{data}, p_{\theta}) & \approx \frac{1}{n}\sum_{i=1}^{n} \frac{1}{2}\left\lVert \nabla_{x}\log p_{\theta}(x_{i}) \right\rVert ^2 + \mathrm{tr}(\nabla_{x}^2\log p_{\theta}(x_{i})) \\ & =\frac{1}{n}\sum_{i=1}^{n} \frac{1}{2}\lVert \nabla_{x}f_{\theta}(x_{i}) \rVert ^2 + \mathrm{tr} (\nabla_{x}^2f_{\theta}(x_{i})) \end{align} \]
问题是,计算 trace 太过 expensive。
Noise Contrastive Estimation
参考 Noise-Contrastive-Estimation
将 \(Z(\theta)\) 看作是一个独立的参数,模型从 \(p_{\theta}(x)\) 变成了 \(p_{\theta, Z}(x)\),最后结果只需要分别采样 \(x_{1},\dots,x_{n} \sim p_{data}(x), y_{1},\dots,y_{n} \sim p_{noise}(y)\),然后计算 NCE loss:
\[ \begin{align} &\frac{1}{n}\sum_{i=1}^{n} [ f_{\theta}(x_{i})-\log \text{sum} \exp (f_{\theta}(x_{i}), \log Z + \log p_{noise}(x_{i})) \\ &\quad \quad \quad \quad + \log Z + p_{noise}(y)-\log \text{sum}\exp (f_{\theta}(y_{i}),\log Z + \log p_{noise}(y_{i})) ] \end{align} \]
推导:

Adversarial Training

Summary







